Складні багатокутники та зірки - еннеаграма, декаграма

Чим простіша фігура, тим частіше вона використовується символічно. Так, багато культур, релігій та організацій використовують кола та трикутники, але набагато рідше - гептаграми та октаграми. Як тільки ми переходимо до восьмикутних зірок та фігур, їхнє використання стає все більш специфічним та обмеженим.

Хоча я обговорюю ці фігури як зірки (поліграми), та ж сама загальна логіка може бути застосована і до форми багатокутника. Наприклад, декагон (10-гранний замкнений багатокутник) може означати те ж саме, що і декаграма (10-кутна зірка), але для простоти я посилаюся лише на декаграми, частково через те, що зірки використовуються частіше.

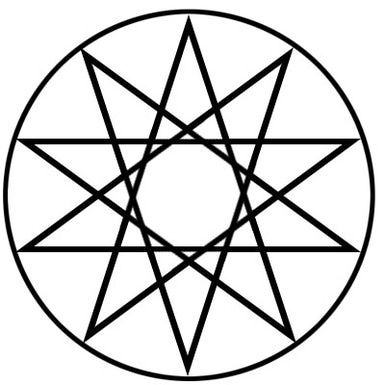
Еннеаграма - 9-кінцева зірка

Термін "еннеаграма" сьогодні найбільше асоціюється з підходом до аналізу та розвитку особистості. В її основі лежить ідея про те, що існує дев'ять типів особистості, які зображені у вигляді неправильної дев'ятикутної форми. Лінії зображують зв'язки та стосунки між типами, а розташування навколо кола дає додаткове розуміння.

Ця ж дев'ятикутна форма була використана у течії, відомій як "Четвертий шлях", що розвинулася в середині 20-го століття.

Віра Бахаї використовує дев'ятикутну зірку як свій символ.

Коли еннеаграма утворена трьома трикутниками, що накладаються один на одного, вона може представляти трійцю трійць і, таким чином, бути символом святості або духовного завершення.

Можливо, хтось може використовувати еннеаграму як символ універсальної цілісності, де кожна точка представляє планету, хоча пониження статусу Плутона з планети до плутоїда тепер ускладнює такий символізм. Можна замінити Плутон на Сонце або Місяць, або вилучити Землю (оскільки це єдина планета, якої немає на нашому небі) і замінити Землю і Плутон на Сонце і Місяць.

9-кутні зірки також іноді називають нонаграмами.

Декаграма/декаграма - 10-кінцева зірка

Для тих, хто працює в рамках каббалістичної системи, декаграма може представляти 10 сефірот Дерева Життя.

Декаграма може бути утворена шляхом накладання двох пентаграм. Це може відображати об'єднання протилежностей, оскільки пентаграми, спрямовані вгору і вниз, можуть мати власне значення. Пентаграма може представляти п'ять елементів, і деякі бачать в кожному елементі позитивний і негативний аспект. Таким чином, будь-яка декаграма (не тільки та, що утворена шляхом накладання пентаграм) може також представляти позитивний аспект.та негативні аспекти п'яти стихій.

Ендекаграма - 11-кінцева зірка

Ендекаграми надзвичайно рідкісні. Єдине використання, про яке мені відомо, - в системі "Золотий світанок", де вони мають вузько технічне і специфічне значення.

Додекаграма - 12-кутна зірка

Число дванадцять має багато потенційних значень. Це кількість місяців у році, що символізує річний цикл, його завершеність і цілісність; це кількість учнів Ісуса, що робить його поширеним числом у християнстві, і первісна кількість єврейських племен, що робить його поширеним числом в юдаїзмі.

Але дванадцятигранна фігура найчастіше представляє зодіак, який поділяється на дванадцять знаків. Ці дванадцять знаків далі поділяються на чотири групи, визначені за стихією (три знаки вогню, три знаки води і т.д.), тому додекаграма, що складається з чотирьох трикутників, що накладаються один на одного, працює особливо добре. Додекаграма, що складається з двох шестикутників, що накладаються один на одного, може бути використана для поділу символів зодіаку за чоловічою статтю.(Гексаграми не можуть накладатися одна на одну, оскільки гексаграми - це трикутники, що накладаються одна на одну. Це те саме, що додекаграма, складена з чотирьох трикутників).